2025. 3. 30. 21:56ㆍ컴퓨터공학 전공공부/알고리즘
정렬 문제에서의 Optimal Solution
- Unsorted data에서 key를 비교해 탐색하는 경우, optimal solution은 $\theta \left( n \right) $번의 비교를 필요로 한다.
- Sorted data에서 key를 비교해 탐색하는 경우, optimal solution은 $\theta \left( \log n \right) $번의 비교를 필요로 한다.
즉, input의 형태에 따라 문제의 복잡도는 변화한다.
Insertion Sort (삽입정렬)
Strategy
n개의 원소를 가진 배열에 대하여 index 1부터 n-1의 원소까지가 삽입되듯이 동작한다. 삽입된 해당 원소가 swap을 이용해 적절한 위치로 이동한다.
Example

- 회색 영역은 정렬된 원소들, 검은색 영역은 현재 삽입되어 정렬될 원소, 흰색 영역은 정렬되지 않은 원소들(아직 삽입되지 않은 원소들).
- 검은색 영역이 index 2~n이 될 때까지 반복. 검은색 영역의 원소가 '삽입되듯이' 동작.
- 검은색 영역의 원소와 바로 앞 원소를 비교하여, 검은색 영역의 원소가 더 작을 경우 swap
Algorithm
void insertionSort(Element[] E, int n)
int xindex;
for (xindex = 1; xindex < n; xindex++)
Element current = E[xindex]; //current는 검은색 영역
key x = current.key; //x는 검은색 영역의 값
int xLoc = shiftVacRec(E, xindex, x);
E[xLoc] = current; //적절한 자리(xLoc)에 current를 저장
return;
int shiftVacRec(Element[] E, int vacant, Key x)
if (vacant == 0) //내가 첫 원소면 자리 유지
xLoc = vacant;
else if (E[vacant-1].key <= x) //내 앞 원소보다 내가 크면 유지
xLoc = vacant;
else //내 앞 원소보다 내가 작으면
E[vacant] = E[vacant-1]; //내 앞 원소가 내 자리로 복사
xLoc = shiftVacRec(E, vacant-1, x); //재귀
return xLoc;Analysis
Worst case analysis
최악의 경우, index i에 있는 원소는 i번의 비교를 수행해야 한다.
따라서 $W \left(n\right) = \sum_{i=1} ^{n-1} i= \frac{n\left(n-1\right)}{2} \in \Theta \left(n^2\right)$
Average case analysis
정렬에서는 실패하는 case가 없다. 따라서 $A \left(n \right) = \sum Pr \left( I _{i} \right) \cdot t \left( I_{i} \right) $
먼저, 어떠한 index i와 그 값 x에 대하여 x가 위치할 수 있는 자리는 index 0~i, 즉 i+1개이다. → $Pr \left(I_{i} \right) = \frac{1}{i+1}$
index i와 그 값 x에 대하여,
| x의 적절한 위치(index) | 비교연산의 수 |
| i (현재 자리) | 1 |
| i-1 | 2 |
| i-2 | 3 |
| ... | ... |
| 1 | i |
| 0 | i |
따라서 $A \left(n\right) = \sum_{i=1}^{n-1} \left( \frac{1}{i+1} \sum_{j=1}^{i}j + \frac{i}{i+1} \right)$ $\approx \frac{1}{4} n^2$
정리하자면, Worst case와 Average case 모두 $\Theta \left(n^2 \right)$이다. 다만 이렇게 최고차항이 동일할 경우 계수까지도 비교하곤 하며, 계수가 $W (n) = \frac{1}{2} n^2$, $A (n) = \frac{1}{4} n^2$이므로 엄밀히 따지면 A(n)이 더 빠름을 알 수 있다.
Optimality
Sorting 알고리즘의 basic operations : 원소 간 비교연산
key의 비교를 통해 정렬하는 알고리즘은 항상 worst case에서 $\frac {n(n-1)}{2}$, average case에서 $\frac {n(n-1)}{4}$개의 비교를 필요로 한다. (n개의 원소에 대해)
Insertion Sort 알고리즘은 인접한 원소들끼리만 swap이 이루어질 때 optimal하다. 다만, 다른 경우에는 optimal하지 않으며, 가장 좋은 정렬 알고리즘은 아니다.
Quick Sort
핵심 전략, Divide and Conquer
Divide and Conquer은 quick sort에서 쓰는 전략으로, 하나의 큰 문제를 여러 개의 작은 문제로 쪼개 푸는 것이다. 여기서 유의할 점은, 문제의 size만 작아지고 같은 문제여야 한다는 점.
전략을 더 구체적으로 설명하자면 다음과 같다.
- 원래 문제를 같은 문제의 작은 사례들로 나눈다(divide).
- 작은 사례들을 재귀적으로 해결한다(conquer).
- 원래 입력에 대한 답을 얻기 위해, 작은 사례에 대한 답들을 합친다(combine).
solve(I)
n = size(I)
if (n <= smallsize) //원하는 size가 됐는지 확인. -> base case
solution = directlySolve(I);
else
divide I into I1, ..., Ik
for each i in {1, ..., k} //재귀적으로 해결
Si = solve(Ii)
solution = combine(S1, ..., Sk);
return solution;
Quick Sort
Quick Sort는 divide and conquer 패러다임에 기반한 무작위 정렬 알고리즘이다.
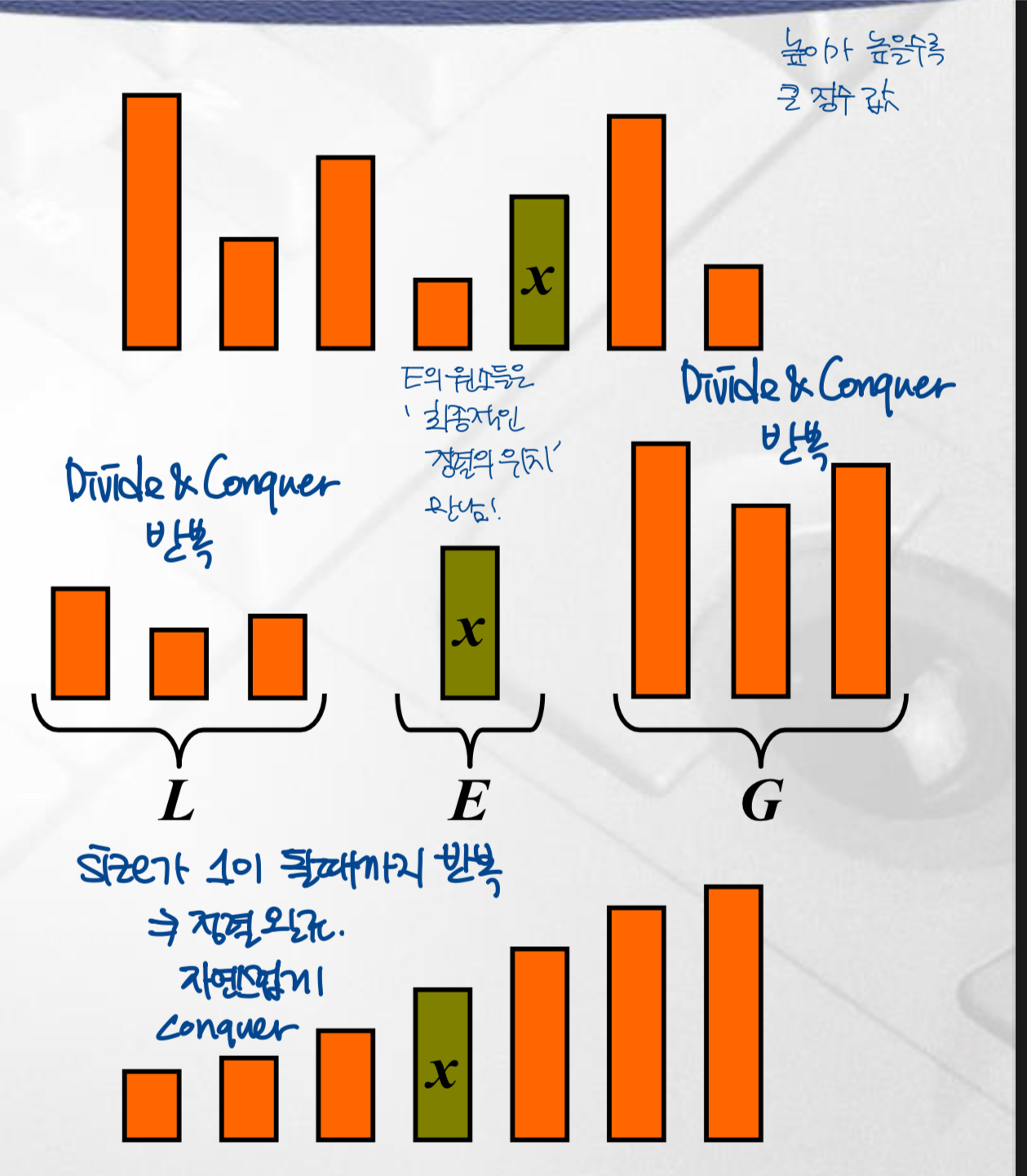
- Divide : 무작위 변수 x (pivot이라 부름)을 선택한다. 이를 기준으로 값들을 세 개의 그룹으로 나눈다.
- L : x보다 작은 값들
- E : x와 같은 값들 → E 그룹은 자연스럽게 conquer된다. 즉 divide를 수행하면 최소 pivot 하나는 정렬된다.
- G : x보다 큰 값들
- Conquer : L, G에 대하여 정렬한다.
- Combine : L, E, G를 합친다.
핵심 step, Partition
Algorithm partition(S, p)
Input sequence S, position p of pivot
Output subsequences L, E, G of the elements of S less than, equal to, or greater
than the pivot, respectively.
L, E, G <- empty sequences
x <- S.remove(p) //pivot을 일단 빼둠 - O(1)time
while not S.isEmpty()
y <- S.remove(S.first()) //원소들을 앞에서부터 빼서 p와 비교 - O(1)time
if y<x
L.insertLast(y)
else if y=x
E.insertLast(y)
else
G.insertLast(y)
return L, E, G삽입과 삭제는 O(1) time에 이뤄진다. 이 과정이 n-1번 일어나므로, quick sort의 partition(divide) step은 O(n) time을 사용한다.
Analysis
Worst case analysis
Worst case는 모든 값이 distinct한 상황에서 pivot이 최솟값 또는 최댓값을 가질 때이다. 이 경우 L, G는 항상 하나는 empty, 하나는 pivot 제외 전부를 포함하게 된다.
이에 따라 최악 수행 시간은 $n + (n-1) + ... + 2 + 1 \approx O(n^2)$이다. (최악의 경우에선 빠른 알고리즘이 아님.)

Average case analysis

위 사진에 따라 Average case에서의 L 그룹 크기를 $\frac {n}{4}$, G 그룹 크기를 $\frac {3n}{4}$로 하자. 그렇다면 아래와 같은 tree를 그릴 수 있다.
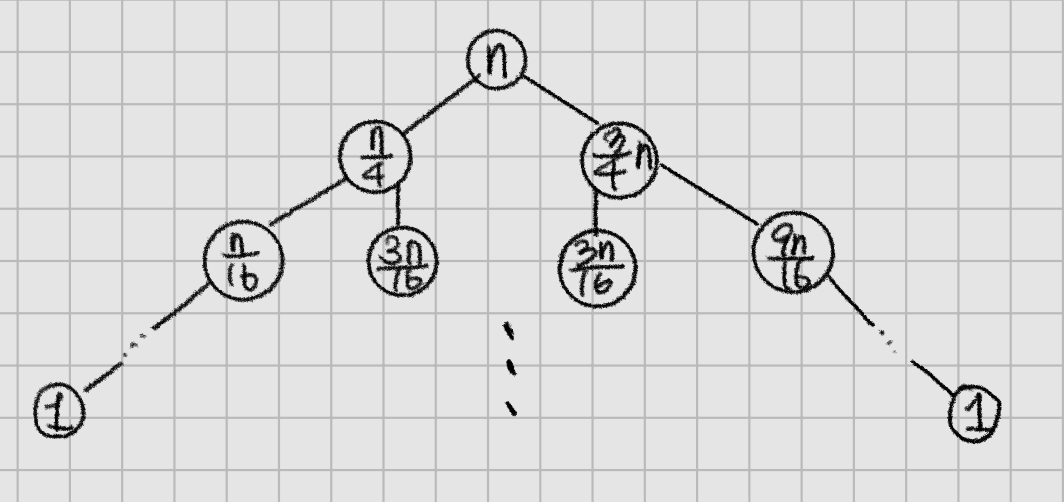
점근적으로 모든 레벨이 O(n) time 수행한다. → tree의 height x n이 총 수행시간이 될 것.
가장 깊은 depth가 tree의 height가 될 것이고, 이는 가장 오른쪽 자식의 depth일 것이다. 따라서, $n \cdot \left( \frac{3}{4} \right) ^{k} = 1$. 정리해보면 $ k \in O(\log n)$이고, 따라서 $A(n) = O(n \log n) $이다.
구체적인 연산과정은 아래와 같다.
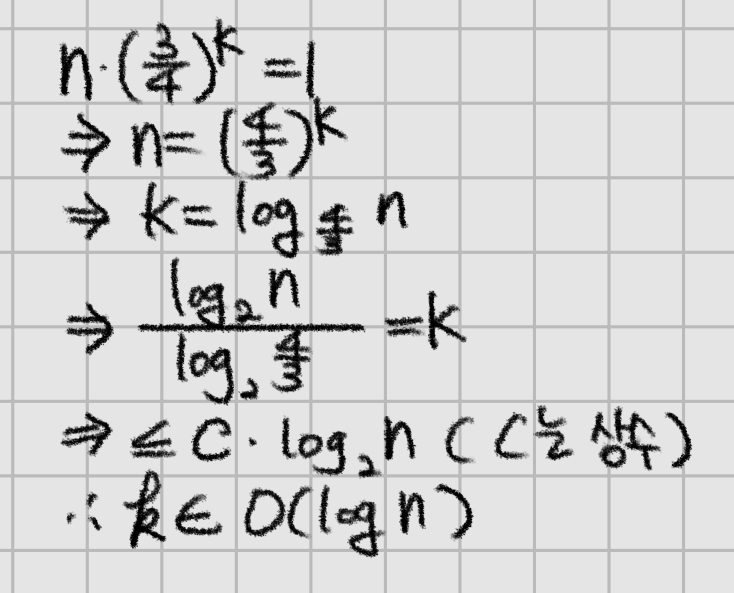
In-Place Quick Sort (제자리 Quick Sort)
In-Place Quick Sort는 추가적으로 사용하는 space가 O(1) space인 quick sort를 말한다. (재귀로 구현하는 경우, O(n) space까지는 in-place로 본다.) 즉 입력 배열에서 swap을 위한 지역변수 외의 space를 사용하지 않는 알고리즘이다.
Algorithm inPlaceQS(S, l, r) //subproblem의 시작 l, 끝 r
//처음엔 l은 0, r은 n-1
Input sequence S, ranks l and r
Output sequence S with the elements of rank between l and r
rearranged in increasing order
if l>=r
return
i <- a random integer between l and r
x <- S.elemAtRank(i)
(h, k) <- inPlacePartition(x) //partition이 in place로 수행
inPlaceQS(S, l, h-1)
inPlaceQS(S, k+1, r)i, x, (h, k)를 수행하는 부분을 visit 함수로 본다면 형태가 preorder traversal과 닮은 걸 알 수 있다.
위 알고리즘을 수행하면, h, k는 E 그룹의 시작과 끝이 되어 아래와 같은 모습이 된다.

In-Place Partitioning
In-Place의 경우, L, E, G로 나누던 quick sort와 달리 $L$, $E \cup G$의 두 그룹으로 문제를 나눈다.

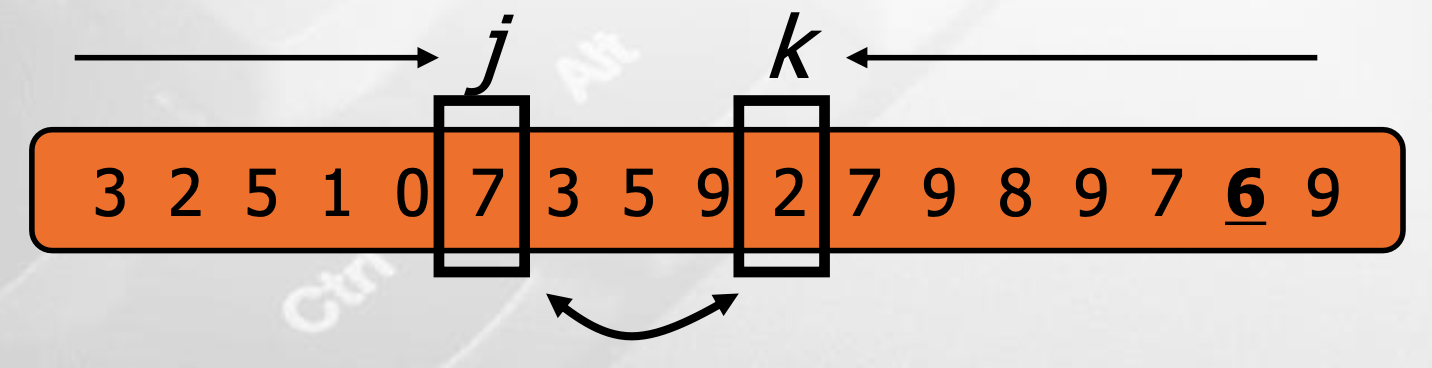
j와 k가 cross할 때까지 아래의 과정을 반복한다.
- pivot(6) 이상 원소를 찾을 때까지 j를 오른쪽으로 이동하며 탐색한다.
- pivot(6) 미만 원소를 찾을 때까지 k를 왼쪽으로 이동하며 탐색한다.
- j와 k를 swap한다. → pivot보다 작은 원소를 다 왼쪽으로 몰아, 왼쪽에는 $L$, 오른쪽에는 $E \cup G$가 위치하게 한다.
j와 k가 cross하면, 마지막으로 j, k가 만난 원소와 pivot을 swap한다.
'컴퓨터공학 전공공부 > 알고리즘' 카테고리의 다른 글
| CH04 : Sorting 4 - Accelerated Heap Sort (0) | 2025.04.07 |
|---|---|
| CH04 : Sorting 3 - Heap Sort (0) | 2025.04.06 |
| CH04 : Sorting 2 - Merge Sort (0) | 2025.04.04 |
| CH02 : 데이터 추상화와 기본적인 자료구조 (0) | 2025.03.27 |
| CH01 : [예시] 정렬된 배열에서의 탐색 알고리즘 (0) | 2025.03.25 |