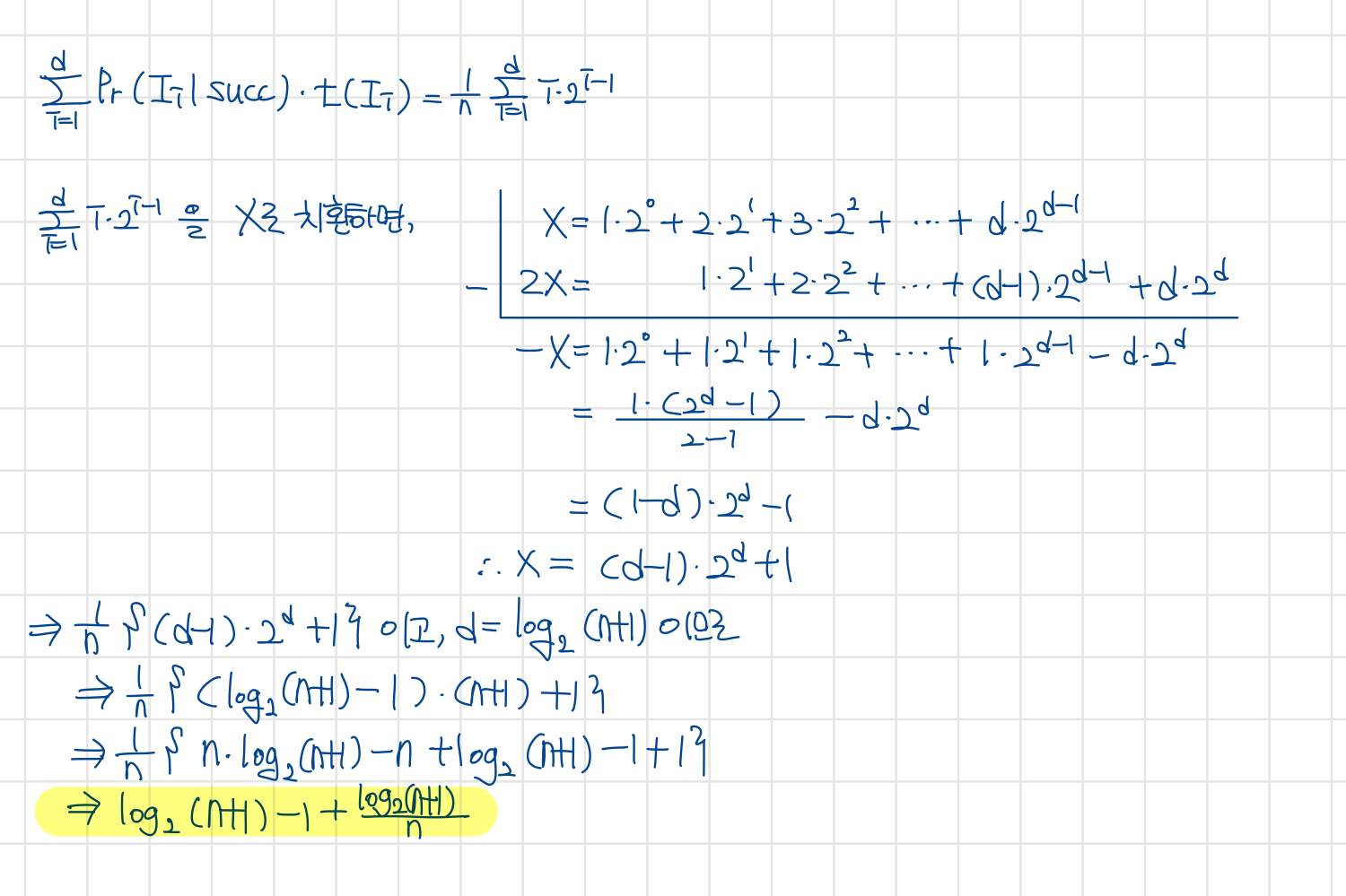2025. 3. 25. 17:11ㆍ컴퓨터공학 전공공부/알고리즘
문제 정의
1. input : 오름차순으로 정렬된 n개의 원소를 가진 배열 E, 값 K
2. output : E에 K가 존재할 경우 K의 index, 그 외의 경우 -1
해결책 A
Strategy A
모든 원소를 순차적으로 확인한다.
Algorithm A
int seqSearch(int[] E, int n, int K)
int ans, idx;
ans = -1; //Assume Failure
for (idx = 0; idx < n; idx++)
if (K == E[idx]) //*basic ops*
ans = idx; //success
break; //done
return ans;Analysis A
Worst Case
$W(n) = n$
- 발생조건 : 배열의 마지막 원소만 K이거나, K가 배열에 없는 경우
Average Case
$A(n) = q\cdot \frac {n+1}{2} + (1-q)n$
- $A(n) = Pr(succ)A_{succ}(n) + Pr(fail)A_{fail}(n)$
- $A_{succ}(n)$
- n개의 case 발생 → 0번째 원소와 match, 1번째 원소와 match, ..., n-1번째 원소와 match
- 모든 case의 발생확률이 동일하다고 가정하면 $Pr(I_{i} | succ)= \frac{1}{n}$
- $t(i) = \begin{Bmatrix}
1 \;\;(case 0)
\\ 2 \;\;(case 1)
\\ ...
\\ n \;\;(case\; n-1)
\end{Bmatrix}$- 따라서 case i에 대해 $t(i)=i+1$
- 결론적으로 $0\leq i <n$, $t(I _{i})=i+1$이고,
- $A_{succ}(n) = \sum_{i=0}^{n-1} Pr(I_{i} | succ) t(I_{i}) = \sum_{i=0}^{n-1} \frac{1}{n}(i+1) = \frac{1}{n} \sum_{i=1}^{n} i = \frac{1}{n} \cdot \frac{n(n+1)} {2} = \frac{n+1}{2}$
- $A_{fail}(n)$
- case가 오직 하나 → $Pr(I | fail) = 1$
- 결론적으로,
- $A_{fail}(n) = Pr (I |fail)t(I) = n$
- $A_{succ}(n)$
따라서 탐색을 성공할 확률을 q라 할 때, $A(n) = q\cdot \frac {n+1}{2} + (1-q)n$
Optimality A
만약 정렬되지 않은 배열이었다면, $F(n) = n$이므로 optimal한 알고리즘이 맞다. 하지만 정렬된 배열에서는 문제의 복잡도가 내려가기에 optimal하다 볼 수 없다. (이 글 하단 참고)
해결책 B
Strategy B
앞에서부터 순차적으로 탐색하는데, K보다 큰 값을 찾으면 그 이후로는 K가 존재하지 않을 것이므로, -1을 반환한다.
Algorithm B
int seqSearchMod(int[] E, int n, int K) //여기서 Mod는 modified
int ans, idx;
ans = -1; //Assume Failure
for (idx = 0; idx < n; idx++)
if (K > E[idx]) //*basic ops1*
continue;
if (K < E[idx]) //*basic ops2*
break; //done
//K == E[idx]
ans = idx;
break;
return ans;Analysis B
Worst Case
$W(n) = n+1 \approx n $
- 발생조건
- K가 가장 마지막 원소인 경우
- basic ops1이 n번, basic ops2가 1번 수행
- K가 존재하지 않는데,
- 마지막 원소보다 큰 경우
- basic ops1이 n번 수행
- 마지막 원소, 그 직전 원소 사이의 값인 경우
- basic ops1이 n번 수행, basic ops2가 1번 수행
- 마지막 원소보다 큰 경우
- K가 가장 마지막 원소인 경우
Average Case
$A(n) = q\cdot \frac {n+1}{2} + (1-q)( \frac {n} {n+1} + \frac {n}{2} )\approx \frac {n}{2}$
- $A(n) = Pr(succ)A_{succ}(n) + Pr(fail)A_{fail}(n)$
- $A_{succ}(n)$
- n개의 case 발생 → 0번째 원소와 match, 1번째 원소와 match, ..., n-1번째 원소와 match
- 모든 case의 발생확률이 동일하다고 가정하면 $Pr(I_{i} | succ)= \frac{1}{n}$
- $t(i) = \begin{Bmatrix}
1 \;\;(case 0)
\\ 2 \;\;(case 1)
\\ ...
\\ n \;\;(case\; n-1)
\end{Bmatrix}$- 따라서 case i에 대해 $t(i)=i+1$
- 결론적으로 $0\leq i <n$, $t(I _{i})=i+1$이고,
- $A_{succ}(n) = \sum_{i=0}^{n-1} Pr(I_{i} | succ) t(I_{i}) = \sum_{i=0}^{n-1} \frac{1}{n}(i+1) = \frac{1}{n} \sum_{i=1}^{n} i = \frac{1}{n} \cdot \frac{n(n+1)} {2} = \frac{n+1}{2}$
- $A_{fail}(n)$
- n+1개의 case 발생 → 각 원소의 앞, 뒤로 가능성이 있으므로
- 모든 case의 발생확률이 동일하다고 가정하면 $Pr(I_{i} | fail)= \frac{1}{n+1}$
- 결론적으로
- $A_{fail}(n) = \sum_{i=0}^{n} Pr(I_{i} | fail) t(I_{i}) = \sum_{i=0}^{n-1} \frac{1}{n+1}(i+1) + \frac{n}{n+1} = \frac{n}{2} + \frac{n}{n+1}$
- $\frac{n}{n+1}$ : 마지막 case에 대해. 마지막 case및 그 직전 case는 basic ops가 n개로 같다. (나머지 case는 i번째 case에 대하여 i+1개)
- $A_{fail}(n) = \sum_{i=0}^{n} Pr(I_{i} | fail) t(I_{i}) = \sum_{i=0}^{n-1} \frac{1}{n+1}(i+1) + \frac{n}{n+1} = \frac{n}{2} + \frac{n}{n+1}$
- n+1개의 case 발생 → 각 원소의 앞, 뒤로 가능성이 있으므로
- $A_{succ}(n)$
따라서 탐색을 성공할 확률을 q라 했을 때, $A(n) = q\cdot \frac {n+1}{2} + (1-q)(\frac{n}{n+1} + \frac{n}{2}) \approx \frac{n}{2}$
Optimality B
Optimality A와 비교하여, worst case가 동일하기 때문에 크게 개선되었다 보기 어렵다.
해결책 C
Strategy C
배열의 중간값을 확인하고, 그 값과의 비교를 통해 배열의 앞 절반, 혹은 뒤 절반을 제거한다. 이 과정을 재귀적으로 반복한다.
Algorithm C
이진 탐색 (Binary Search)
- input : E, K, first, last
- E는 정렬된 배열이며, 범위는 first부터 last까지이다. K는 찾으려는 key 값이다.
- 이러한 input에 대하여 input size n은 항상 last - first + 1이다.
- ouput : E에 K가 존재할 경우 K의 index, 그 외의 경우 -1
int binarySearch(int[] E, int first, int last, int K)
//종료조건 (base case)
if (last < first) //K와 비교할 원소가 없는 경우
idx = -1;
//recursive case
else
int mid = (first+last)/2;
if (K == E[mid]) //*basic ops1*
idx= mid;
else if (K < E[mid]) //*basic ops2*
idx = binarySearch(E, first, mid-1, K); //last = mid -1
else //*basic ops3*
idx = binarySearch(E, mid+1, last, K); //fisrt = mid +1
return idxAnalysis C
모든 basic ops에 대해 1번의 비교가 됐다고 가정 → 각각이 n개씩 수행되어 3n이 수행되었다고 해도 점근적으로 n에 근사하기에
모든 basic ops는 K 값과 배열의 원소 값을 비교하는 '비교 연산'이다.
Worst Case
$W(n) = \log{n}$
위 알고리즘에선 '비교 연산 수행 →탐색 영역 절반으로 줄임'이 반복된다. 따라서 탐색 영역이 1이 될 때까지 비교 연산을 수행한다고 볼 수 있다.
- $n \times \frac{1}{2} \times \frac{1}{2} \times \cdots \times \frac{1}{2} = 1$이고, $\frac{1}{2}$는 k번 곱해진다.
- $n \times \left (\frac{1}{2} \right) ^k =1$, $k= \log{n}$
따라서 $W(n) = \log{n}$이다.
Average Case
$A(n) \approx \log { \left( n+1 \right) } -q$
- $A(n) = Pr(succ)A_{succ}(n) + Pr(fail)A_{fail}(n)$
- Assumption → worst case를 가정
- $Pr(I_{i} | succ) = \frac{1}{n}$ (모든 성공 case의 발생확률은 동일)
- $Pr(I_{i} | fail) = \frac{1}{n+1}$ (모든 실패 case의 발생확률은 동일)
- $n=2^d -1$ (항상 complete binary tree 꼴을 가정)
- 모든 원소는 distinct (중복으로 인해 원소를 빨리 찾는 경우를 배제)
- $A_{succ}(n)$
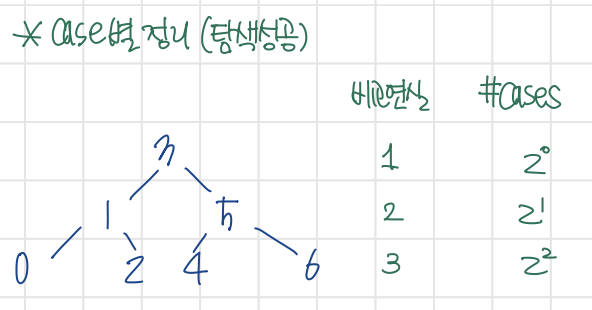
- 모든 index에서 K가 발생할 수 있으므로 n case
- $\sum_{i=1}^{d} Pr\left( I _{i} | succ \right) \cdot t(I_{i}) = \frac{1}{n} \sum_{i=1}^{d} i \cdot 2^{i-1}$
- $d=\log _{2} {\left(n+1\right)}$이므로 $\log \left(n+1\right) + \frac {\log \left(n+1\right)} {n} -1$
- (참고) $t(I_{i}) = i \cdot 2^{i-1} $인 이유
- 구체적인 연산과정은 다음과 같다.
- $A_{fail}(n)$
- 모든 gap에서 K가 발생할 수 있으므로 n+1 case
- $\sum _{i=1}^{d} Pr \left(I_{i} | fail \right) \cdot t \left(I_{i} \right) = \frac {1}{n+1} \cdot d \cdot (n+1)$
- 즉, $d= \log (n+1) $
- 모든 gap에서 K가 발생할 수 있으므로 n+1 case
- Assumption → worst case를 가정
따라서 탐색을 성공할 확률을 q라 했을 때, $A(n) \approx \log { \left( n+1 \right) } -q$. 구체적인 연산과정은 아래와 같다.
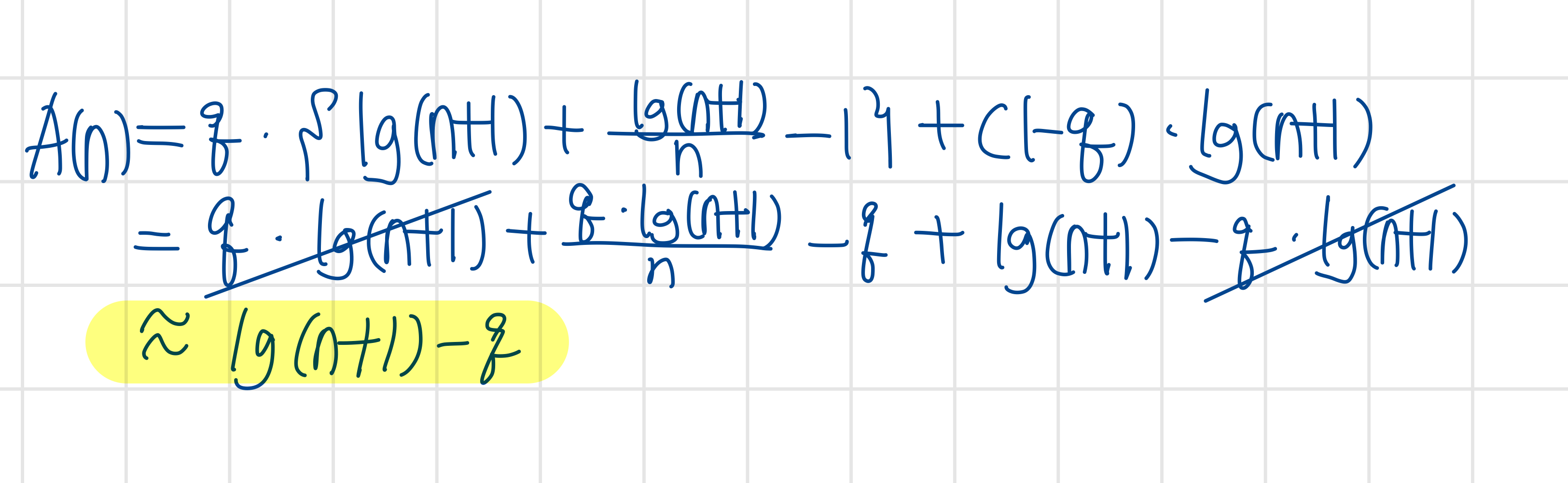
Optimality C
문제의 복잡도
알고리즘 C의 최적성을 검증하기 위해, 이 문제의 복잡도를 먼저 계산해보자.
이 알고리즘의 class는 비교(comparison)이므로, decision tree를 이용해 문제의 복잡도를 계산해 보겠다. (비교연산 기반의 문제 복잡도는 주로 decision tree를 활용해 확인한다.)
- decision tree의 규칙
- 트리의 root는 배열 중 첫 번째 비교에 쓰이는 원소의 인덱스이다.
- 특정한 노드 X의 자식에 대하여,
- 왼쪽 자식 : K<E[i] → K가 X보다 작다.
- 오른쪽 자식 : K>E[i] → K가 X보다 크다.
- K==E[i]일 경우 자식은 없다.
이에 따라, 각 알고리즘의 decision tree를 그려보면 다음과 같다.
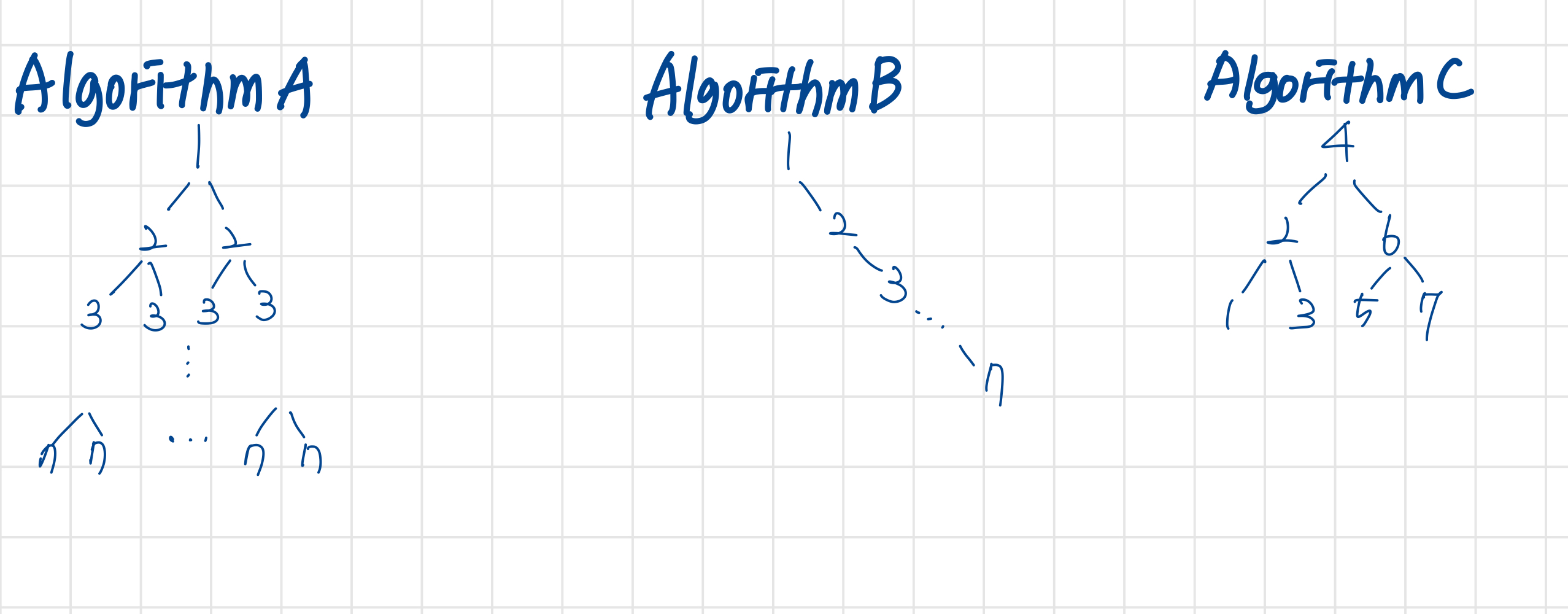
Algorithm C의 Optimality with Decision Tree
worst case는 root부터 leaf까지의 제일 긴 path이다. 이를 p라 하자.
decision tree에 N개의 노드가 있다고 할 때, $N \leq 1+2+4+ \cdots + 2^{p-1}$ →$N \leq 2^{p} -1$, $2^{p} \geq (N+1)$
한편 $N \geq n$이므로, $2^{p} \geq (N+1) \geq (n+1)$, $p \geq \log (n+1)$
따라서 Algorithm C는 optimal하다 볼 수 있다.
- (참고) $N \geq n$의 증명
- 모순법으로 증명 : $N < n$을 가정
- i번째 원소의 값이 K(찾고자 하는 값)인 배열 E1과 i번째 원소의 값이 K'(not K)인 배열 E2에 대하여, 배열의 다른 요소가 동일하다(원소 수, 다른 원소의 값)고 가정하자.
- $N < n$임에 따라 i를 탐색하지 못한다고 하면, E1과 E2의 결과값이 모두 탐색 실패이므로, 가정이 모순이다.
- 모순법으로 증명 : $N < n$을 가정
'컴퓨터공학 전공공부 > 알고리즘' 카테고리의 다른 글
| CH04 : Sorting 4 - Accelerated Heap Sort (0) | 2025.04.07 |
|---|---|
| CH04 : Sorting 3 - Heap Sort (0) | 2025.04.06 |
| CH04 : Sorting 2 - Merge Sort (0) | 2025.04.04 |
| CH04 : Sorting 1 - Insertion Sort, Quick Sort (0) | 2025.03.30 |
| CH02 : 데이터 추상화와 기본적인 자료구조 (0) | 2025.03.27 |