2025. 4. 6. 22:26ㆍ컴퓨터공학 전공공부/알고리즘
Heap
Heap의 조건
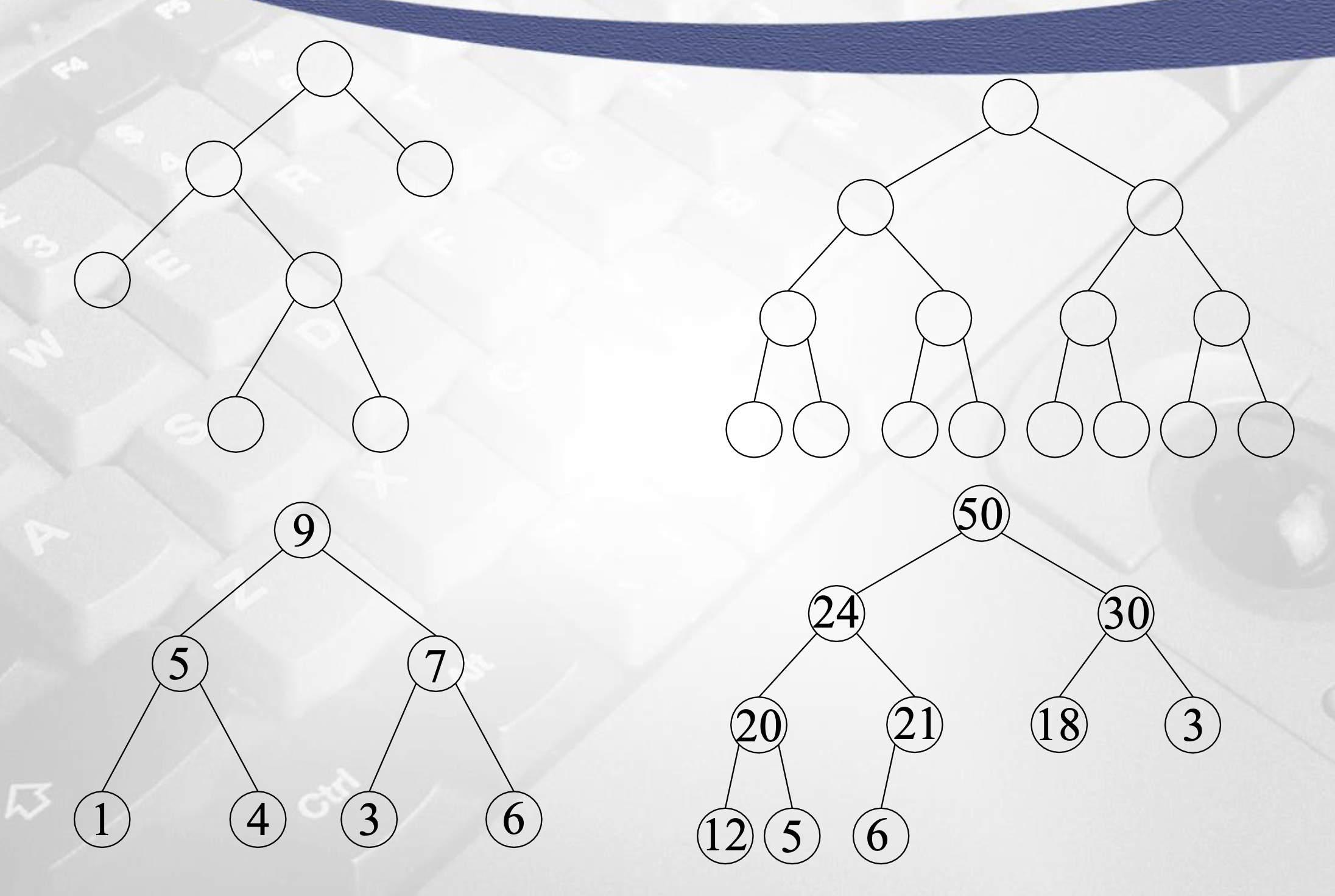
Heap이 되기 위한 조건은 다음의 두 개이다.
- 구조조건 : complete binary tree
- height h에 대하여, h-1까지는 complete tree (꽉 찬 트리)
- 모든 leaves는 depth h나 h-1에 위치, depth h의 leaves는 왼쪽부터 채워진다.
- 순서조건 : partial order tree property
- maxheap 기준, parent의 key 값이 나보다 크거나 같아야 한다.
- minheap일 땐 parent의 key 값이 나보다 작거나 같아야 한다.
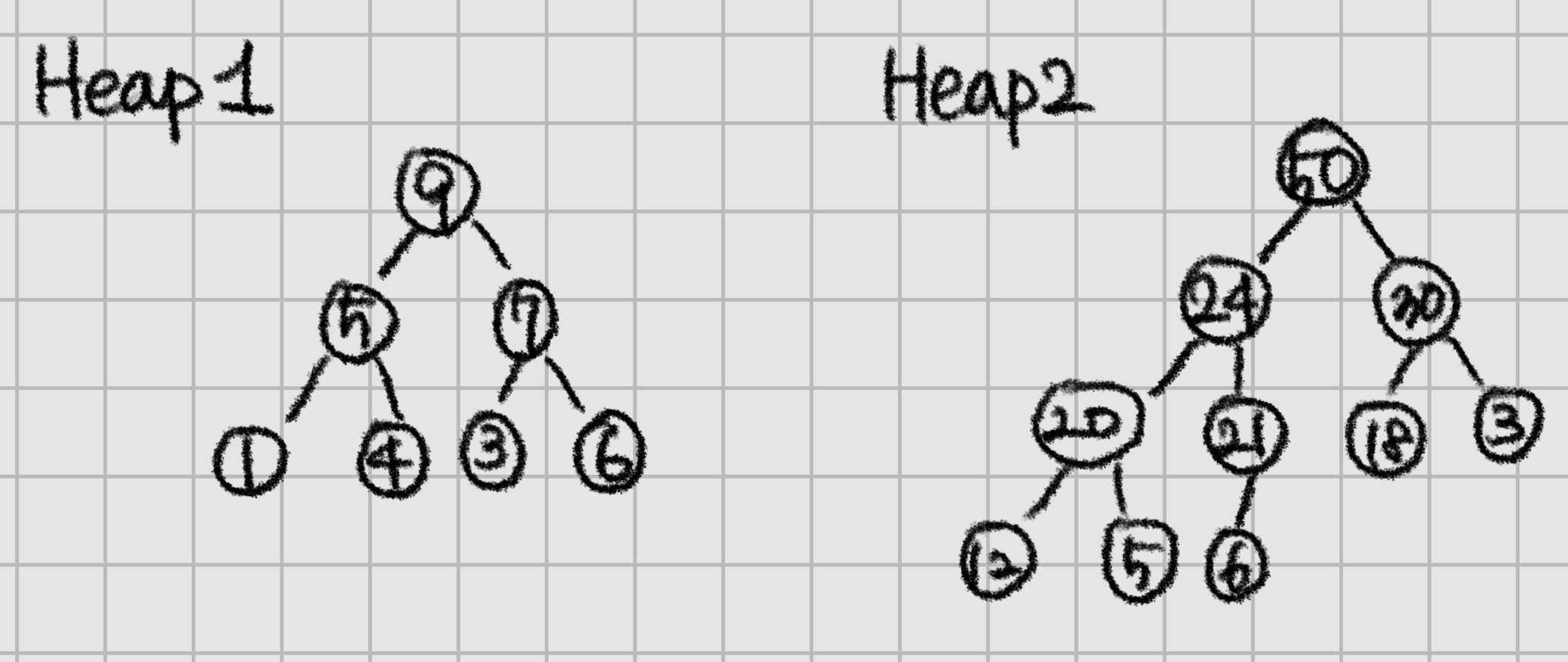
아래는 heap인지, 아닌지를 구분하는 예시이다.
Heap ADT
| 삽입 : insert() | 삭제 : deleteMax() *max heap 기준 |
탐색 : getMax() *max heap 기준 |
|
| W(n) | $O( \log n)$ | $O( \log n)$ | $O( 1)$ |
삽입
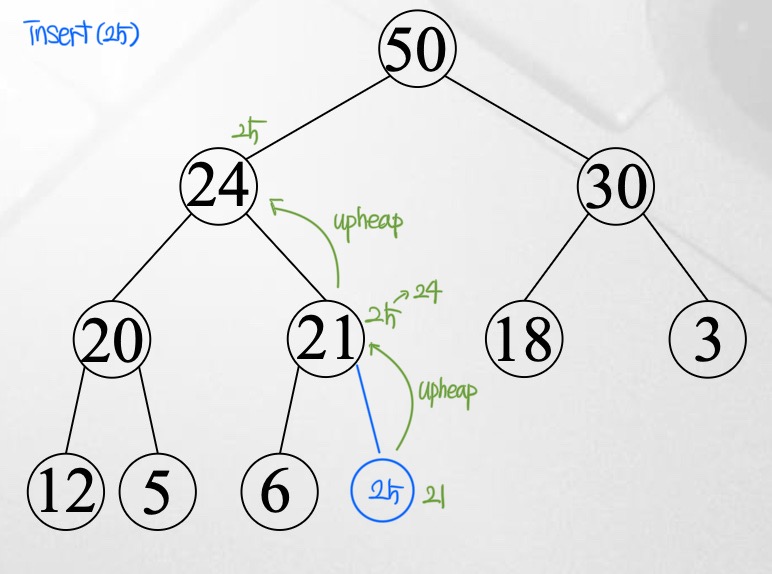
가장 아래 depth에서 왼쪽부터 채우며 노드를 삽입한다. 이후 upheap을 통해 순서를 정렬한다. upheap은 본인의 key값과 부모의 key값을 비교하여 본인의 key값이 더 크면 swap하는 것이다.
여기서 basic operation은 원소 간 비교연산이고, height $h \in O(\log n)$이다. (∵complete binary tree) → 따라서 $W(n) = O (\log n)$.
삭제
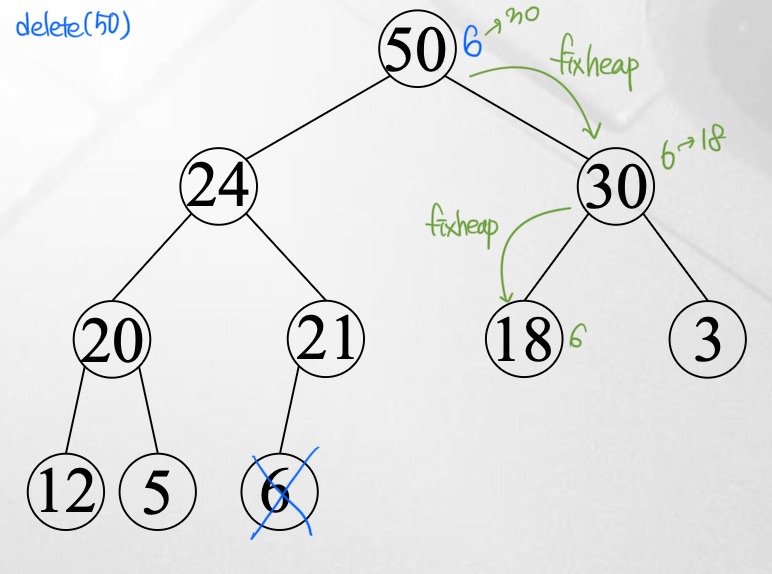
last node의 값을 루트에 복사하고, last node를 삭제한다. 이후 fixheap(==downheap)을 통해 순서를 정렬한다. downheap은 본인의 key값과 큰 자식의 key값을 비교하여 본인의 key값이 더 작으면 swap하는 것이다.
여기서 basic operation은 원소 간 비교연산이고, height $h \in O(\log n)$이다. (∵complete binary tree) 한편 worst case에서 큰 자식을 찾는 비교 h번, fixheap을 위한 비교 h번해서 총 2h번의 비교가 일어난다. → 따라서 $W(n) = W(2h) \approx O (\log n)$.
탐색
getMax의 경우 root의 값을 가져오면 되므로 $W(n) = O (1)$.
Heapsort
Heapsort 전략
배열의 모든 원소를 heap에 삽입한다.(n번의 insert) 이후 getMax()와 deleteMax()를 반복하여 원소를 정렬한다.(n번의 정렬) → 결론적으로 heapsort는 worst case에서 $O (n \log n)$ time을 요하므로 문제의 복잡도와 같아 optimal algorithm이다.
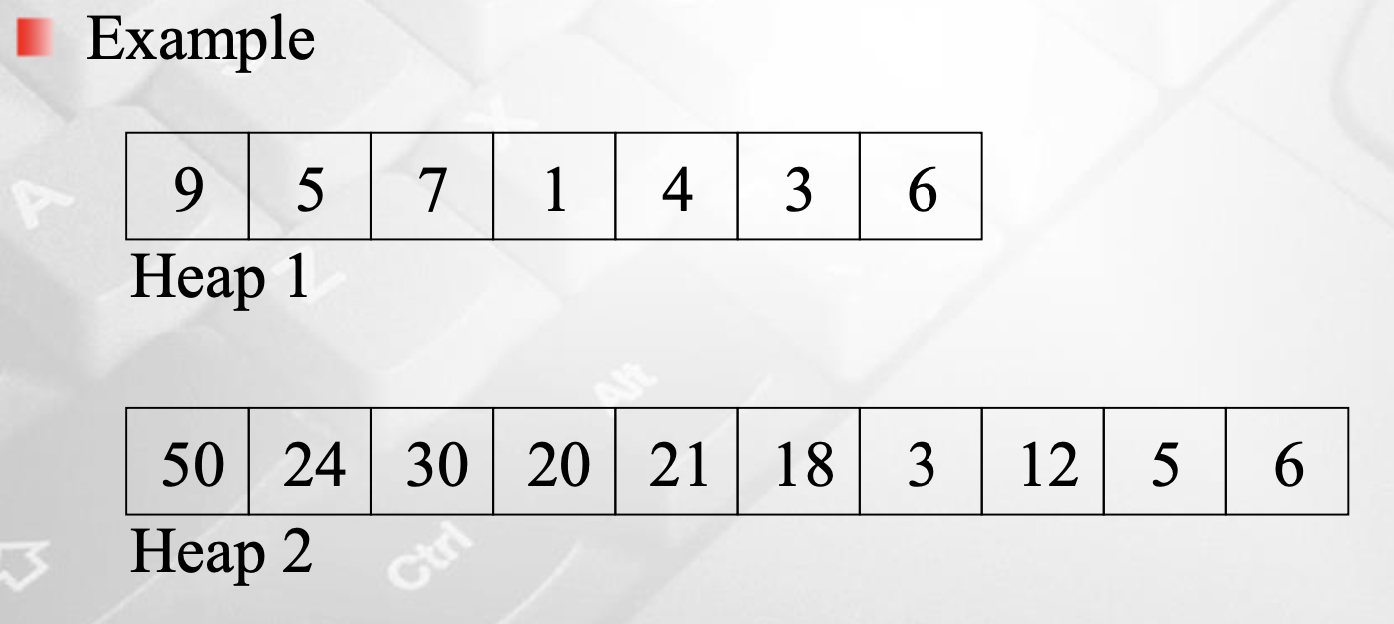
배열을 통한 heap 구현
'배열의 모든 원소를 heap에 삽입한다.' → heap과 배열이 어떻게 매칭되는 것일까?
다음의 규칙을 따라 매칭된다.
- 배열 E는 1,...,n까지의 원소를 갖는다. (index 0은 사용하지 않음.)
- index i에 대하여
- index 2i는 i의 왼쪽 자식
- index 2i+1은 i의 오른쪽 자식
- index $\left \lfloor \frac{i}{2} \right \rfloor$는 i의 부모
In-place Heapsort
배열을 max heap으로 변환 후, getMax()의 값을 마지막 원소와 swap한다. 이를 통해 제일 뒤에서부터 정렬 완료된 값이 순차적으로 채워진다. 이렇게 되면 배열 외 별도의 메모리 공간을 사용하지 않기 때문에 in-place heapsort가 가능하다.
Heapsort Algorithm & Analysis
heapSort(E, n)
construct H from E, the set of n elements to be sorted
for (i=n; i>=1; i--) //뒤에서부터 채움
curMax = getMax(H)
deleteMax(H)
E[i] = curMax- Analysis
- construction of heap : O(n) time
- getMax() : O(1) time
- deleteMax() : O(2h) time
- E[i]에 curMax 저장 : O(1) time
- 따라서 주목해야할 부분은 1. construction of heap - O(n) time / 2. deleteMax() n번 반복 - O(2h *n) time
void constructHeap(H)
if (H is not a leaf)
constructHeap(left subtree of H) //현재 노드의 왼쪽 자식에 대한 재귀
constructHeap(right subtree of H) //현재 노드의 오른쪽 자식에 대한 재귀
Element K = root(H)
fixHeap(H, K)
returnfixHeap을 visit 함수로 본다면, postorder traversal 형태임을 볼 수 있다. 또한 bottom up 방식의 construction이다.
deleteMax(H)
copy the rightmost element of the lowest level of H into K //last node를 K에 복사
delete the rightmost element on the lowest level of H //last node 삭제
fixHeap(H, K)fixHeap(H, K) //**important**
if (H is a leaf)
insert K in root(H)
else
set largerSubHeap to leftSubtree(H) or rightSubtree(H), whichever has larger key at
its root. This involves one key comparison.
if (K.key >= root(largerSubHeap.key))
insert K in root(H)
else
insert root(largerSubHeap) in root(H)
fixHeap(largerSubHeap, K)
return- 동작 설명
- H가 leaf면, 즉 H가 자식이 없으면 K를 힙의 root에 넣고 return
- H가 leaf가 아니면,
- 왼쪽 subtree, 오른쪽 subtree 중 root의 key값이 큰 subtree를 'largerSubHeap'으로 설정
- 내 key 값이 largerSubHeap의 key 값보다 크거나 같으면 → 순서조건 만족하는 상황
- K를 힙의 root에 넣고 return
- 내 key 값이 largerSubHeap의 key 값보다 작으면 → 순서조건 불만족하는 상황
- largerSubHeap을 가지고 다시 fixHeap (재귀)
- Analysis
- 위의 Heap - Heap ADT - 삭제에서 얘기했듯, deleteMax()는 $W(n) = W(2h) \approx O (\log n)$ time을 요한다. (정확히는 $2 \log n$)
Heapsort Final Analysis
k개의 노드를 갖는 heap에 대하여 fixHeap은 $2 \log (k)$ time이 걸린다. 따라서 모든 삭제연산에 대하여, $2 \sum_{k=1}^{n-1} \log k \in \Theta \left(n \log n \right)$ time이 걸린다.($2 \log n$ time이 걸리는 연산이 n회) 결론적으로 $W(n) = 2n \log n + O(n)$ (삭제 연산 + heap 생성 시간).
'컴퓨터공학 전공공부 > 알고리즘' 카테고리의 다른 글
| CH04 : Sorting 5 - Radix Sort (0) | 2025.04.13 |
|---|---|
| CH04 : Sorting 4 - Accelerated Heap Sort (0) | 2025.04.07 |
| CH04 : Sorting 2 - Merge Sort (0) | 2025.04.04 |
| CH04 : Sorting 1 - Insertion Sort, Quick Sort (0) | 2025.03.30 |
| CH02 : 데이터 추상화와 기본적인 자료구조 (0) | 2025.03.27 |