2025. 4. 14. 18:36ㆍ컴퓨터공학 전공공부/알고리즘
Dynamic sets는 동적인 원소 집합으로, 시간의 흐름에 따라 원소의 개수가 변화하는 집합을 말한다. 이러한 dynamic sets의 구현에서 필요한 array doubling에 대해 알아보고, array doubling을 합리적으로 분석할 수 있는 기법인 amortized analysis(분할 상환 분석)에 대해 알아보려고 한다.
Array Doubling
Array Doubling이란?
array는 사용할 크기를 미리 결정한다는 특성이 있다. 이에 따라 임의의 index에 상수 시간 접근이 가능하다는 장점이 있지만, array의 size가 불필요하게 많이 남거나 필요한 공간보다 부족한 상황이 발생할 수 있다는 단점도 있다. Array Doubling은 array size가 부족할 때 기존 array의 크기를 두 배로 늘려주는 것을 말한다.
Array Doubling Strategy
- 기존 배열 A의 array size n을 넘어서는 원소 x가 하나 들어왔을 때,
- 새로운 2n짜리 배열 B를 만들고
- A의 원소 n개를 B에 옮기고
- B에 x를 넣는다.
- 마지막으로 A를 삭제하고, B의 시작 주소를 A에 저장한다.
Array Doubling의 cost
기존 배열의 크기 n에 대하여 n+1개의 원소가 들어왔을 때 array doubling이 야기된다. transferring cost를 t라 하면
- array doubling에 드는 cost는 t*n
- 지금까지 발생한 총 transferring cost, 즉 이전의 array doubling cost는 t*n
- $t\cdot \frac{n}{2} +t \cdot \frac{n}{4}+ t \cdot \frac{n}{8} + \cdots + t \cdot \frac{n}{n} = tn \cdot \sum_{i=1}^{\log n} \frac{1}{2^i}$
- $ \leq tn \sum _{i=1}^{\infty} \frac{1}{2^i}$
- $= tn \cdot \frac{ \frac{1}{2}} {1- \frac{1}{2}}$
- $= tn$
결론적으로 array doubling의 total cost는 현 step의 tn + 이전 steps의 tn = 2tn을 능가할 수 없다.
Amortized Analysis
Amortized Analysis가 왜 필요한가?
쉽게 얘기하자면, 배열에 값을 집어넣는 경우 array doubling은 굉장히 드물게 일어난다. 하지만 array doubling으로 인해 worst case에서의 cost는 크게 늘어난다($O(1)$ time → $O(n)$ time) . 즉, worst case의 값 단 하나로 분석하는 게 합리적이지 못하다는 것이다.
마찬가지로, 아래는 다른 예시이다.
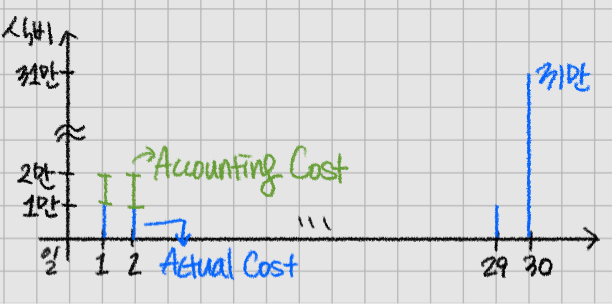
이 예시의 경우 30일의 소비로 인해 worst case는 31만원이다. 다만, 1~29일은 1만원씩만 쓰기에 worst case의 값 단 하나로 분석하기엔 합리적이지 않다. 따라서 '단 한 번의 큰 소비'를 고려할 수 있는 amortized analysis가 적절하다.
Amortized Analysis
amortized analysis는 어떤 연속적으로 발생하는 연산에 대해, 최악의 경우에 그 연산의 평균 비용을 제공한다. amortized analysis에는 크게 세 가지 방법이 있다.
- aggregate method, 산술 평균 방식
- 총 60만 / 30일 = 2만원
- accounting method, 회계 방식
- potential method
아래에선 accounting method를 기준으로 설명하겠다.
참고로, amortized analysis와 average case analysis 모두 '평균' 개념이 들어가는데, 둘의 제일 큰 차이점은 '확률'이다. amortized analysis에서는 확률 개념이 들어가지 않지만, average case analysis엔 확률 개념이 들어간다.
Amortized Analysis (Accounting Method)
Amortized cost = actual cost(실 사용 금액) + accounting cost(저축 비용)
- Actual cost
- 실제 사용하는 금액
- Accounting cost
- 연산마다 accounting cost는 다르다.
- 다음의 점을 고려하여 설정한다.
- 합법적으로 수행된 모든 동작에 대해 accounting costs의 총합은 0 이상 양수여야 한다.
- 분석이 수월하도록 고려하여 accounting cost를 할당한다.
Amortized Analysis 예시
식비 문제

매일 사용하는 1만원이 actual cost, 30일에 1만원 + 30만원의 소비를 위해 매일 저축하는 1만원이 accounting cost이다.
array doubling 문제 - array로 구현한 stack에서의 push 동작 상황에서 amortized analysis
- actual cost
- array doubling이 발생하지 않는 상황에서, actual cost = 1
- array doubling이 발생하는 상황에서, actual cost = 1+tn
- 이 때는 기존에 W(n) 분석하던 방식으로 구하면 된다.
- n+1번째 원소 x를 push하는 비용 1
- n개의 원소를 t비용에 transfer하는 비용 t*n
- 이 때는 기존에 W(n) 분석하던 방식으로 구하면 된다.
- accounting cost
- array doubling이 발생하지 않는 상황에서, accounting cost = 2t
- 기존 배열(size n)도 이전 배열(size $\frac{n}{2}$)에서 doubling됐을 것이다. 따라서 doubling되어 가져온 $\frac{n}{2}$ 제외 나머지 공간인 $\frac{n}{2}$에 대해 push연산 발생할 때마다 얼마씩 저축해야할지 계산한다.
- $\frac{n}{2} \times$ (저축비용) $= tn$, (저축비용) = 2t
- 기존 배열(size n)도 이전 배열(size $\frac{n}{2}$)에서 doubling됐을 것이다. 따라서 doubling되어 가져온 $\frac{n}{2}$ 제외 나머지 공간인 $\frac{n}{2}$에 대해 push연산 발생할 때마다 얼마씩 저축해야할지 계산한다.
- array doubling이 발생하는 상황에서, accounting cost = -tn +2t
- -tn : 실제 doubling으로 인해 소모되는 비용
- 2t : 새로운 값(원소 하나)를 저장할 때 저축하는 비용
- array doubling이 발생하지 않는 상황에서, accounting cost = 2t
- amortized cost
- array doubling이 발생하지 않는 상황에서, amortized cost = 1+2t
- array doubling이 발생하는 상황에서, amortized cost = 1+tn-tn+2t = 1+2t
- 따라서 push동작의 amortized cost는 1+2t이다.
- 정리하자면, W(n) = O(n), amortized W(n) = O(1+2t). t가 상수이면 O(1)이다.
- 기존 분석과 비교하기 위해 amortized 분석에 대해선 앞에 'amortized'를 명시한다.
- 정리하자면, W(n) = O(n), amortized W(n) = O(1+2t). t가 상수이면 O(1)이다.
'컴퓨터공학 전공공부 > 알고리즘' 카테고리의 다른 글
| CH06 : Dynamic Sets and Searching 3 - Red-Black Tree (0) | 2025.04.18 |
|---|---|
| CH06 : Dynamic Sets and Searching 2 - Binary Search Tree (0) | 2025.04.16 |
| CH04 : Sorting 5 - Radix Sort (0) | 2025.04.13 |
| CH04 : Sorting 4 - Accelerated Heap Sort (0) | 2025.04.07 |
| CH04 : Sorting 3 - Heap Sort (0) | 2025.04.06 |