CH06 : Dynamic Sets and Searching 3

컴퓨터공학 전공공부/알고리즘

CH06 : Dynamic Sets and Searching 3 - Red-Black Tree

말랑흰두부 2025. 4. 18. 20:27

Balanced Binary Search Tree의 대표적 예 중 하나인 Red-Black Tree를 알아보려 한다. (BST에 대한 설명은 다음 링크를 참고 : https://malangdubu-tech.tistory.com/29)

Red-Black Tree란?

이름처럼, 각 노드가 Red 혹은 Black의 색깔을 가지게 된다. 다음의 특징을 만족하는 BST이다.

root property : root는 black
external property : 모든 leaf는 black
internal property : red 노드의 자식은 black
- black의 자식은 red, black 둘 다 가능
depth property : 모든 leaf는 같은 black depth를 가짐.
- black depth : root 노드부터 해당 노드까지의 path 상에 있는 black edge 수
  - black edge : black 노드에서 부모로 향하는 edge

Red-Black Tree의 Height

n개의 원소를 갖는 complete binary tree에 대하여 height $h \in O(\log n)$이다.

한편, n개의 원소를 갖는 red-black tree는 항상 complete binary tree는 아니다. path의 길이를 비교했을 때 가장 짧은 path는 해당 path에 오로지 black 노드만 있는 경우일 것이고, 가장 긴 path는 red, black 노드가 번갈아 나타나는 경우일 것이다. 하지만 depth property에 의해 가장 긴 path에서 red 노드의 개수는 black 노드와 같을 것이다. 따라서 red-black tree의 height $h_{rb} \leq 2h$이고, 점근적으로 $h_{rb} \in O(\log n)$임을 알 수 있다.

Red-Black Tree에서의 Search

red-black tree에서의 search는 기본적인 BST에서의 search와 방식이 같다. →상단 링크의 Binary Searh Tree Algorithm 부분 참고.

red-black tree에서는 $h_{rb} \in O(\log n)$이므로 search time이 $O(\log n)$로 보장된다.

Red-Black Tree에서의 Insertion

삽입되는 형태

red-black tree 및 보통의 BST에서는 key-value pair, 즉 entry 형태로 원소를 삽입한다. 따라서 BST를 dictionary의 구현에 사용하곤 한다. → STL 중 map은 red-black tree로 구현돼 있다.

Insert Strategy

삽입하려는 원소 k를 leaf z까지 내린다.
1. root부터 시작 : k의 값과 노드의 값을 비교하여, k의 값이 작으면 left로, 크면 right로 차례차례 내려간다. k와 같을 때는 left, right 중 하나로 내려가야 하는데, (수업에선) right를 기준으로 한다.
z에 있던 기존 노드를 제거하고, k + 두 개의 black leaf로 이루어진 subtree를 그 자리에 삽입한다.
1. k는 무조건 red 노드로 삽입한다.
double red를 해결한다. (아래에서 별도 설명)

Insert와 Red-Black Tree Property

red-black tree의 insertion에서 중요한 건, insertion 이후에도 red-black tree의 property를 만족해야 한다는 점이다. insertion 상황에서 각 property에 대해 살펴보도록 하겠다. 참고로, 이러한 property 만족이 용이하기에 위와 같은 strategy를 따르는 것이다.

root property : 만약 root에 삽입한다면, 그 경우에만 삽입하는 노드를 black으로 바꿔주면 된다. root에의 삽입 case만 따로 처리해주면 되므로, root property 만족은 크게 어렵지 않다.
external property : 항상 black leaf 두 개를 같이 삽입하기에, 항상 만족한다.
depth property : 삽입한 subtree를 보면, k를 red로 삽입하기 때문에 black edge의 수가 변하지 않아 black depth도 변하지 않음을 알 수 있다. 즉, 항상 만족한다.
internal property : 이 property는 만족하지 못할 가능성이 있어 따로 처리해줘야 한다. →double red

Double Red

Double Red란 red 노드의 자식으로 red 노드가 위치하는 상황으로, internal property를 위반하게 된다. 크게 두 가지로 나눌 수 있다.

삽입한 노드 z와 z의 부모 v, v의 형제노드 w에 대하여,

w가 black인 case : restructuring으로 해결
w가 red인 case : recoloring으로 해결

Restructuring

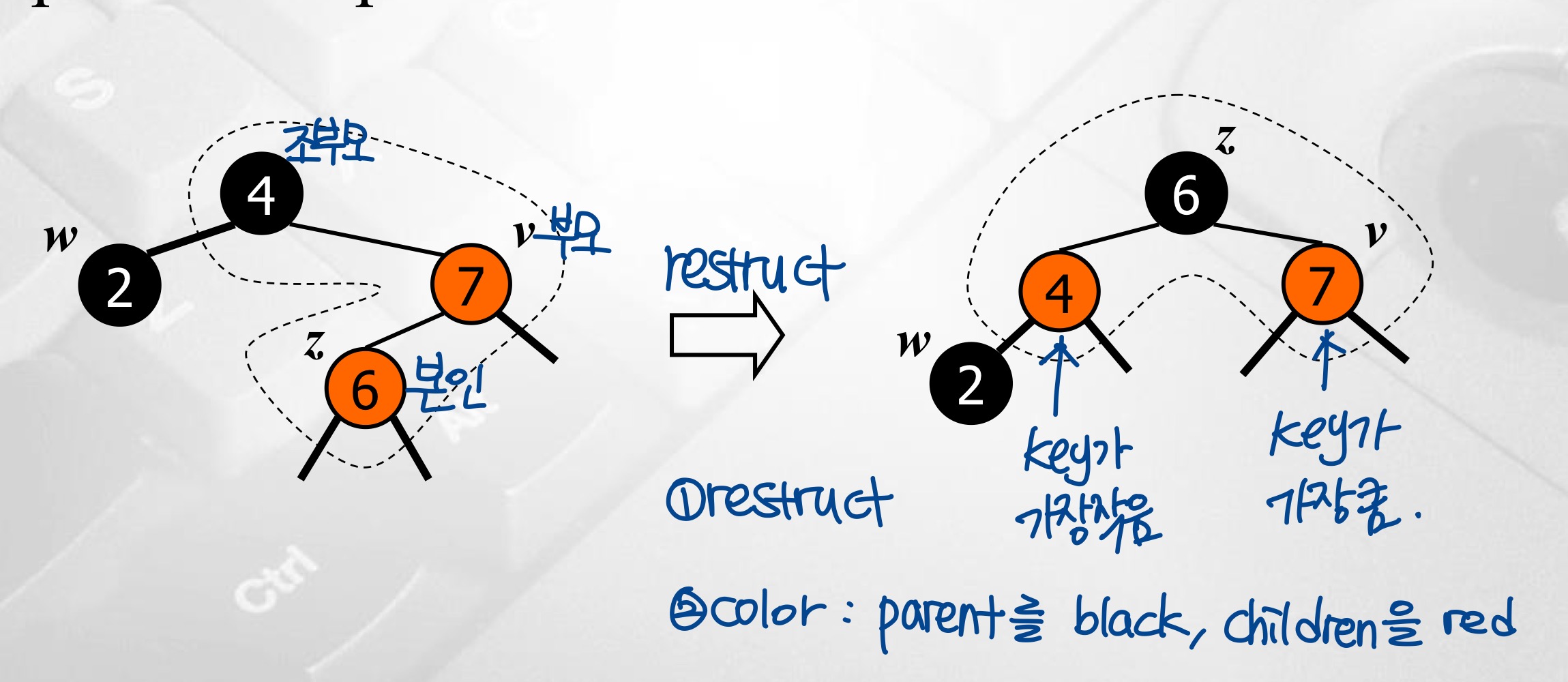
삽입한 노드 z와 z의 부모 v, v의 형제노드 w, z의 조부모에 대하여 z, v, 조부모를 비교해 크기가 제일 작은 값을 left child로, 중간 크기를 부모로, 크기가 제일 큰 값을 right child로 재구성한다. 이후 부모를 black, 두 자식을 red로 칠한다.

한편, restructuring후 각 노드의 subtree들도 적절히 배치해줘야 한다! 각 subtree들의 상대적인 순서가 유지돼야 한다.

추가로, 만약 노드들의 값이 중복인 경우엔 어떻게 처리해야 할까?

inorder traversal 순으로 처리한다. (visit 순서가 inorder traversal이기 때문)

(참고) 아래는 네 가지의 restructuring 경우이다. 이처럼 문제 상황은 다르나 같은 구조로 귀결될 수도 있다.

Recoloring

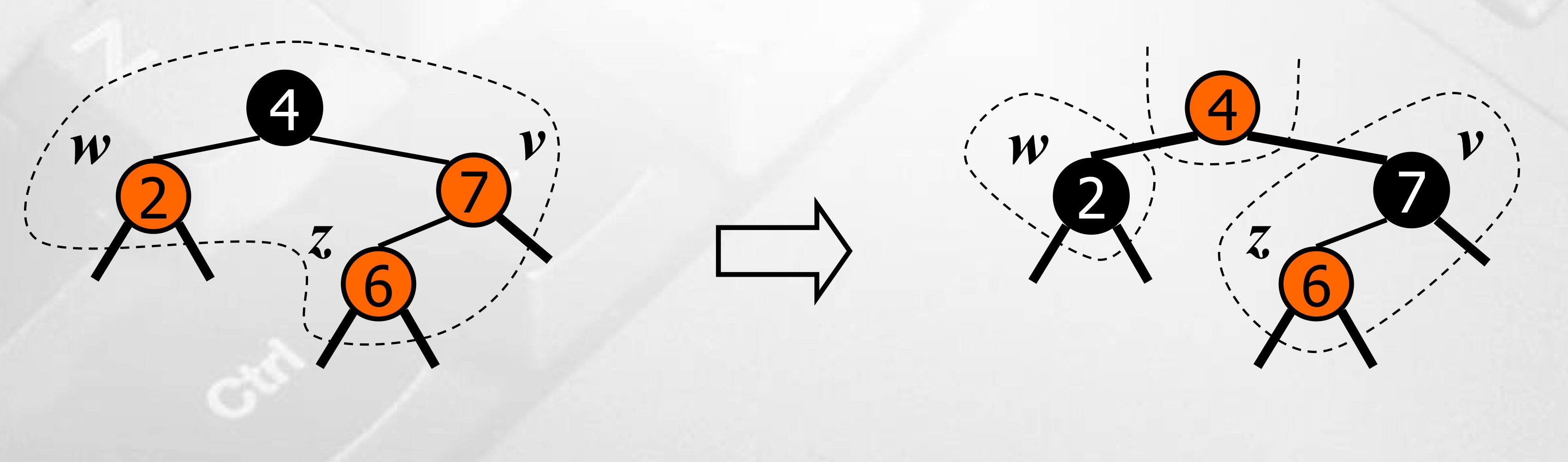
삽입한 노드 z와 z의 부모 v, v의 형제노드 w, z의 조부모에 대하여 v, w를 black으로 + 조부모를 red로 칠한다. (root는 예외) 다만 조부모가 red로 변하기 때문에 조부모와 고조부모 사이 double red가 다시 발생할 수 있다. → double red의 propagation. 이 경우 recoloring을 재귀적으로 수행하여 해결한다.

Insert Algorithm & Analysis

Algorithm insertItem(k, o)

1. Search for key K to locate the insertion node z
2. Add the new item (k,o) at node z and color z red
3.
    while doubleRed(z)
        if isBlack(sibling(parent(z)))
            z <- restructure(z)
        else //sibling(parent(z)) is red
            z <- recolor(z)

Analysis

step 1 : height만큼의 노드를 탐색하며 z를 찾아야 한다. $h = O(\log n)$이므로 O(log n)
step 2 : O(1)
step 3 : O(log n)
- restructuring : 한 번 수행에 O(1)이 걸리며 double red가 propagate되지 않으므로 O(1)
- recoloring : 한 번 수행에 O(1)이 걸리지만, double red propagation으로 인해 최악의 경우 root까지 올라가며 recoloring해야 하므로 O(h) → O(log n)

결론적으로 O(log n) time이 걸린다.

Red-Black Tree Insertion Example

아래는 red black tree에 원소들이 삽입되는 예시이다. 구체적인 설명은 생략.